突然ですが問題です。

2辺の長さがa,bで面積がAの長方形がある。この外周の長さが最小となるa,bの値を求めよ。
a,bの長さに関係なく、面積が一定なら外周の長さも同じような気もしますが、正解はa=b=√A、 要するに正方形です。建築にあてはめて考えてみると、屋根勾配がないハコ型の建物なら、正方形の平面形状にすると最も表面積が少なくて済み効率的、というになります。
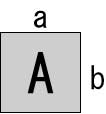
構造設計の面からみても、極端に細長い建築物は短手方向の耐力を確保しにくく、建物内部に壁が増えたり、特殊な設計が必要になる場合があります。建築のローコスト化については延べ床面積の大きさや建材のグレードばかり問題になりますが、実は建物の形状も重要な要素です。
とはいえ、自由に建物の形状や配置を考えられる広大な敷地は日本には少なく、いわゆる「うなぎの寝床」に代表されるような、間口が狭く奥行きが長い敷地がたくさんあります。うなぎの寝床は狭い隣地境界沿いの難しい工事や、密集市街地における準防火地域対応など、コスト高にならざるを得ない要因が他にもたくさんあり、設計が非常に難しいのですが、デザイン的には特徴的で面白い建築を計画しやすいので、悩ましいところです。
【高校生並み証明】
A=abよりb=A/a
外周長さは
2a+2b=2a+2(A/a)
=2(a+A/a)
相加平均・相乗平均の関係より
a+A/a≧2√(a・A/a)
⇔a+A/a≧2√A
等号成立はa=A/aの時⇔a=√Aのとき (このときb=√A)
よって外周長さ
2a+2b≧4√A
最小となるときのa=b=√A
こんなもんでしょうか。。



